Foreign, sick science
By Bobby Neal Winters
As I stood looking at the body on the table, waiting for Suzanna Doughcoup, our local homicide detective, to arrive, I began to examine my own character more closely.
Why do I find it so hard to say no when someone asks me for a favor?
Why is this especially difficult when it has something to do with mathematics?
Why do I even consider these things when it is something so far out of my area of expertise?
I could find no answers, at least none that I wanted to accept, but I will have to admit I don’t do my best thinking within the cold, antiseptic, rather creepy confines of a morgue.
The call had come at 4am. I staggered to the phone which is placed some distance from my bed. As badly as I hate getting woken up by the phone, it is much worse when it is right by my head.
I don’t remember saying hello but I must’ve because the voice on the other end of the phone spoke to me.
“Hello,” it said. It seemed to be vaguely feminine.
“What?” I replied.
“Hello,” the voice came back and called me by name. “This is Detective Suzanna Doughcoup.”
“Who?” I asked. I still wasn’t taking this in.
“Detective Suzanna Doughcoup,” she said. “I need your help to determine a time of death.”
“Death?” I was really doing rather badly. “Time? What time is it?”
“It’s 4am,” Detective Doughcoup answered. “But that’s not important. What I need is for you to help me with a calculation of a time of death. Will you do it?”
Four in the morning is really not a good time for me. I get in some of my heaviest REM sleep in along about them.
“Do it?” I asked. My inflection must have been off a little because I don’t think Suzanna heard the question mark on the end of that.
“Great!” she said. “I will either come to get you or send a car. That will take about half an hour.”
She hung up the phone.
I looked back at the bed which was beckoning to me. It was singing whatever song Circe sang to Odysseus. It was singing it quite well too. I almost yielded to it, but I had a vision of Detective Suzanna Doughcoup battering down my front door and dragging me to the police station in my underwear.
I pulled on my blue jeans, a t-shirt, and my tennis shoes. Then I went to the kitchen and made a pot of coffee. The coffee was done and I’d filled a thermos with it by the time I saw the squad car roll up.
It took the coffee time to perk, and, during that time, I got on the Internet to look up information on time of death calculations. During that brief interval of time, I was able to find five different ways of estimating the time of death: pallor mortis, livor mortis, algor mortis, rigor mortis, and decomposition.
Pallor mortis is paleness and it begins fifteen minutes after death and lasts until two hours after death. Livor mortis is a settling of the blood in capillaries in a way that causes purplish discoloration; maximum discoloration is 6 to 12 hours after death. Rigor mortis starts approximately three hours after death and lasts for approximately three days. I couldn’t even make myself look up the details on decomposition; Detective Doughcoup would strictly be on her own if decomposition were involved.
The remaining one, algor mortis, interested me the most. Algor mortis is the cooling the body that follows death. Using a mathematical formula, one can estimate the time of death. I’d seen it on all my favorite detective shows, but I’d never had the occasion to look it up.
I thought that I knew how it was done. When I’d taught differential equations a number of years ago, I came upon Newton’s Law of Cooling, named for none other than Sir Isaac Newton. As the story goes, an apple hit him on the head and he discovered Newton’s Law of Gravity. I can only imagine that someone threw some cold water on him and he discovered the Law of Cooling.
In plain language, it states that the colder the environment is than an object, the quicker the object cools off. That sounds like common sense and it is common sense, but when you translate it into mathematics it looks more mysterious:
Here the thing on the left hand side of the equation that looks like a fraction is the rate of change of temperature with respect to time.
On the right hand side, the h is a constant that depends on the physical substance being cooled. Metal cools quicker than wood, for example.
The A is the surface area that is exposed. Something that exposes more surface area will cool more quickly than something with less surface area.
The
on the right hand side, represents the difference between the environmental temperature and the temperature of the object. The colder the environment is, the quicker the object cooler.
Quite frankly, the possibility of applying this equation was making my mouth water. The solution involved logarithms, and logarithms are cool.
I will admit that logarithms get a bad rap in our popular culture. In the movie An Officer and a Gentleman, one of the characters refers to them with a participle that begins with the letter “f.” In Roughing It, Mark Twain calls one of his not-too-bright traveling companions a logarithm.
I’ve been of the opinion that giving them the name “logarithms” was a huge marketing mistake. They should’ve called them “happy numbers” or something, but I digress.
In any case, I’d gotten excited about the prospect of using logarithms and expected to see them in the formula used to calculate time of death. Imagine my surprise when I find Newton’s Law of Cooling alluded to only in passing and am presented with the Glaisters Equation instead.
The Glaisters Equation is:
On the left hand side, the little t is the time since death. On the right hand side, the TR is the rectal temperature of the cadaver. I suppose it is hard to get them to put the thermometer under their tongue.
The taking of the temperature is the hardest part of this formula. You subtract the rectal temperature from 98.4--I wonder why not 98.6--and divide by 1.5.
This is incredibly easy. It is so easy that even Suzanna Doughcoup ought to be able to do it. Upon her arrival, I had rehearsed the line that she could go to the Devil and that I would go back to bed.
There was a gentle knock on the door. I opened it prepared to deliver what seemed to be a delicious line.
But it wasn’t her. It was one of her loyal assistants who I knew would stay until I went with him. I packed my line back up--along with my thermos of coffee--and got into the squad car with him.
It is only about five minutes from my house to the police station. It’s not that I live particularly close to the police station; it’s just that nothing is more than about five minutes from the police station.
But, in those five minutes, I began to wonder about the simplicity of the Glaister Equation. It doesn’t take into account the environmental temperature and it doesn’t take into account the surface area of the body. Both of these are important factors in Newton’s Law of Cooling.
As we got closer to the morgue, this worried me less and the rectal part worried me more. I suppose that messing with a dead guy’s fanny is less awkward than messing with a live one’s as there would need to be fewer apologies afterward, but still: eeeewwww.
That last syllable was coursing through my brain when I set foot into the morgue and looked toward an autopsy table. It was covered with the classic white sheet I expected, but there wasn’t nearly as much under that white sheet as I thought.
My first thought was “woman” because women are smaller. But this was really small. It was so small, in fact, and had such a shape that I shook my head in wonder at my earlier estimation of woman.
I turned to the patrolman beside me.
“Armadillo?” I asked.
“Armadillo,” he confirmed. He did so, amazingly, with a straight face. That straight face was put a lie to when he stepped out of the room and began to guffaw.
I stood there by the table asking why, why, why until Detective Doughcoup showed up.
“Glad that you could make it,” she said, “but I am sorry we don’t need you.”
“What?” I was to furious to go beyond monosyllables.
“Yep,” she said, “someone attempted to rob a liquor store and they ran over this armadillo when they made their get away. I thought that a time of death calculation would help establish the time of the crime, but then they told me the clerk had looked at his watch.”
I looked at my watch as a preparation for establishing her time of death, but decided I’d rather go back to bed instead.
“If you’d like to do it anyway, you are welcome to,” she said.
I looked at the thermometer and at the lump under the sheet.
“Take me home,” I begged.
“Have it your way,” she said.
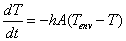







1 comment:
I think there's an error in the law of cooling formula. As best I can read it, it says that when the environment is hotter than the object, the object's temperature will decrease, which hardly matches my experience.
Post a Comment