The Black Box

By Bobby Neal Winters

Part 1; The Big Dance

It had been one of those evenings.  I’d sat down at my desk to write a C++ program. I did this because I am trying to convince myself that I can still learn, can still use my mathematical skills to solve problems.  Writing computer programs is a good way to exercise that particular demon, at least for a while.  
Computers don’t care about your feelings.  They don’t want anything from you.  With computers it is either right or wrong, yes or no, 1 or 0.  There is no maybe, kinda sorta.  This goes a long way to explaining why math and science types are they way they are, but I digress.
After an evening of this quasi-mathematical activity, I went to bed with the TV on and set to go to sleep after about a half-hour.  I almost said after about a half hour, but it is run by a computer.  There is no about a half hour.  It either is or it isn’t.
There was a movie on the TV.  I forget which one exactly.  (I am not a computer.) But it was a cowboy movie and a musical kind of like Oklahoma! but a different one.  I remember nothing beyond that because I drifted off into sleep and in my sleep, I dreamed.
In my dream, I was high above the world over a flat plain and it was night.  Before me upon the plain--which was green but not the green associated with grass--was a rectangular black barn.  The barn was completely black except for a non-descript sign on the roof that read “The Black Box.”
I gradually lost altitude, coming closer to the barn, as was I did I noticed people.  There were two lines of people.  In my dream, I was floating with my body parallel to the ground.  The rectangular barn had its long axis running from left to right.  The people in the dream were arranged in two lines, each line running parallel to the left-right axis of the building.  One line was above the barn and the other line was below it.
Drawing closer, I noticed they were all wearing cowboy hats.  Getting even closer, I notice that the ones above the barn had braided ponytails, so they must’ve been girls, and the ones below the barn did not, so they must’ve been boys.  And all of them were carrying candles.  Some of the candles were lit and some weren’t.
Both lines were moving toward the barn with a rhythmic motion; they were dancing.  I then noticed there were doors in the sides of the barns.  I noticed this when each of the rhythmic cowboys and girls danced their way into them.
Then, in the manner of dreams, I was suddenly in the barn without ever having gone through a door.  Once inside, I saw that the cowboys and cowgirls were facing each other, still dancing in place.   In between them were children.  They were also dressed in traditional cowboy accoutrements, but they were androgynous.  While a particular one on the other might have had a ponytail or not, I couldn’t tell.  It wasn’t important to the dream.
Once lined up facing each other, with one little “cow-child” looking up at each couple the following ritual began to take place.  It started on the right end and proceeded in turn to the left.  
Each member of the couples had a candle as did the child and between each of threesome and the next was a pole that held the barn up with a lantern hanging from it.  With some of the cowboys and cowgirls both candles were lit, in some neither, and in some one and not the other, and to begin with, none of the lanterns were lit nor any of the children’s candles.  
When it became a particular couple’s turn they would look at their candles and look at the lantern to their right.  If exactly none were lit, they would do nothing.  If exactly one was lit, they would light the child’s candle.  If exactly two were lit, they would light the lantern to their left and leave the child’s candle unlit.  If all three were lit, they would light the child’s candle and then light the lantern.  Then the next couple took its turn. The first couple didn’t have a lantern to their right to look to, but acted as if they did and as if it were unlit.
At the end, as in the manner of dreams, certain things began to go out of focus while other things came in.  The cowboys, cowgirls , and lanterns faded into the background while the children came into focus, each holding his/her own candle whether lit or unlit.
Then I started awake because a cat was crawling across my face and muttered something about computer programming before bed..
In the cold light of the next morning, I realized this dream was about how binary addition works.  That is to say, how computers add numbers.  For computers, buried deep beyond where most users dare venture, numbers are represented as binary numbers, ones and zeroes. Instead of the place values representing one, ten, one hundred, etc from right to left, the places represent 1, 2, 4, 8, etc.
The binary number 10110 is 0 times one, 1 times two, 1 times four, 0 times eight, and 1 times sixteen; this represents the number twenty-two.  If this number were to be added to the binary 01101--thirteen--we could carry out the operation as below:

Lanterns	1	1	1	0	0	0
Cowboys	0	1	0	1	1	0
Cowgirls	0	0	1	1	0	1
Children	1	0	0	0	1	1

This is a multi-stage process.  Each stage has three inputs: bit (binary digit) from the first summand; bit from the second summand; and the bit that is carried in.  Each stage has two outputs: the bit that goes into the sum and that bit that is carried to the next stage.  So twenty-two plus thirteen is thirty-five.
This turns addition into a mechanical process.  Mechanical operations yield a result that can be interpreted as a number.  When we type numbers, usually base ten, into a computer, this is what goes on behind the mask as it were.  At least this is how I thought about it for years.
But behind this mask, there are other masks.

Part 2; The Logical Mask

Behind the mask of binary arithmetic is the mask of symbolic logic.  The symbols 1 and 0 can be interpreted to have the truth values of true and false, respectively.  These symbols can be combined using the logical operators of & (and), OR (or), and ~(not), and the statements obtained from these various operations can be evaluated as being either true or false. Consider the following:
“Red is a color” and “Dogs are mammals.”  Each of the these statements is true and the combined statement is true.  However, “Red is a color” and “Dogs are reptiles” is a false statement because the second statement is false.  One can put this into symbols as 1&1=1 and 1&0=0, respectively.  We can summarize these in tables as below:

&	0	1
0	0	0
1	0	1

OR	0	1
0	0	1
1	1	1

x	~x
0	1
1	0

We see the 1s and the 0s are transformed in different ways with each of these operations and this might make us think about how they interact with each other in binary addition. Using this to capture addition adds additional (HA!) complexity which is why it is hidden behind a mask.
It is at this point where those of you who get motion sick in the movies might want to skim for a while.
The addition of one bit to another actually requires two stages because of the having to deal with whatever is being carried in from the previous stage.  The first stage is called a half adder and it requires two pieces as well: sum and carry.
Think about how we add numbers when we do it by hand. We place our numbers one above the other with the digits having the same place value lined up.  We proceed column by column.  We add together the digits from the current column and we add in the carry from the previous column.
To describe this, I am going to have to label various bits, and to keep it from looking too much like algebra class, I will refer to the names in the story I began with.
When we add together those two bits in the column under consideration, the cowboy bit and the cowgirl bit, the only time there will be a carry is when both bits are 1.  So the carry to the next column--at least before we add in the carry from the previous column--is (cowboy bit)&(cowgirl bit). We will call this the left lantern bit.  Don’t go to thinking we are done with the left lantern bit; it will change before this is over.
Let us now worry about what we give to the child. It’s not so straightforward. If exactly one bit from the cowboy or cowgirl is 1, then the child bit is 1.  Here it looks like OR. However, when both bits are 1 then the child bit is 0.  It doesn’t look like anything we’ve seen before from out logical operations.  However, we can create a new operation by compounding the others to take care of this.  It is called exclusive or and it is denoted XOR.  We can define it by the formula:

a XOR b= (a OR b) & (~(a & b)).

There is a reason for the mask, no?
We set the child bit as (cowboy bit) XOR (cowgirl bit).  Again, don’t grow too attached because child bit will change once before we are done. This is because we must now account for the possibility of a carry from the previous stage.  
(Breath, just breath.  In and out, that’s okay.)
We simply add the carry from the previous stage--right lantern bit-- to the child bit.  This means the final bit that we write down for the some will be (child bit) XOR (right lantern bit).  What happens to the carry to the next column--the left lantern bit--is a bit more subtle.  When we sum the child bit (not the new child bit but the old child bit) with right lantern bit, this creates a carry of its own that is to be added to the carry that we originally generated by adding the cowboy bit to the cowgirl bit. (Did you get that bit?) That carry is:

(child bit) & (right lantern bit).

While it might seem that summing this with the left lantern bit would be,

[(child bit) & (right lantern bit)] XOR (left lantern bit),

The fact is that because of the small number of possibilities for right lantern bit, cowboy bit, and cowgirl bit, there will never be a time when the quantities on the left hand side and the right hand side of this XOR will ever be the same.  As a consequence it is:

[(child bit) & (right lantern bit)]  OR (left lantern bit) .

If you have been paying attention to this, you should be just a little dizzy. Air sickness bags are available from the seat back in front of you.

Part 3; Beneath the Mask of Logic, Transistors

Let us now recall that all of this is to get a computer to add numbers together.  In the computer, the numbers are represented by electricity.  One represents where there is current and zero represents where there is not.  This is a mask too, but I will not remove it until the last section. 

We represent the wiring in symbols.  For example, NOT is represented by:

 

& is represented by:

 
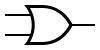
OR is represented by

:
and XOR is denoted by:

 
To spare you further suspense, the wiring the denotes addition is represented by:
For any of you readers who are still there, we are already well past any reasonable threshold of complication.  However, this diagrams still represents a mask because none of those symbols actually stands for a single component.  Rather, they stand for a collection of electronic components that are wired together in a particular way.
One way to make them work is to use something we’ve all heard of but very few think much about: the transistor.
A transistor is a switch, and there are a few different kinds.  The kind I am going to tell you about is the NPN.  An NPN transistor has three legs pictured as below:
Notice the legs are labeled E, B, and C.  This is for emitter, base, and collector.  Think of electricity as coming in C (the collector--they are working with us) and going out E (the emitter--it works). Think of B as an on-off switch (base? on-off switch? they were doing so nicely).  We send in one current through C to E and when we send another current to B, it will turn the switch on and allow it to pass.  When we turn that switch off, it will not.  
This is represented in a wiring diagram by the figure  below:

 

By wiring transistors together in various imaginative ways, we can create the logical gates as pictured above. For example the NOT gate can be wired as:

 

Part 4; Burning Your Fingers

A good question at this point would be how does this circuit yield NOT as an output.  The answer goes as follows.  There is current coming in from the top, all the time.  When there is no signal sent in through the input, i.e. when it is false or 0, the current cannot go through the transistor because it is off.  Therefore it puts out a current, i.e. a true or a 1.  That is to say 0 input gives 1 as an output.  
By way of contrast, if there is a current coming in through the base, i.e. it is true or 1, then current can flow through the transistor from C to E.  This will be the path of least resistance so the current will not go out through the output.  Therefore, there will be no output current.  Therefore, it will be false or 1.  So 1 input gives 0 output.  This is what the NOT gate is supposed to do.
Except its NOT that simple. How do I know?  I wired it on a breadboard with a transistor, resistors, batteries, the whole shooting match.  It took me awhile to get it to work.  Why?  I didn’t use resistors at first.  Resistors are simple--but handy--little things.  They are cheap.  Their purpose is to slow electricity down.  When you don’t have them, the transistor gets hot and doesn’t work well anymore.
How do I know it gets hot?  I burned my finger on it, that’s how.  I got a little transistor-sized blister.
Oh, and the path of least resistance thing.  That’s not exactly true.  It will go through the transistor, but you need to be careful about the amount of resistance in the output direction.  Regardless of that, there will still be a little current.  I never got the resistance high enough so that, although the LED I hooked up to check for current did dim, it never went entirely out.  I suspect you can calibrate things so that you can’t see the LED light but there will still be a tiny amount of current.  
So the 1 and the 0, true and false, are simply masks themselves.  True means the current is above a certain threshold and false means the current is below it.

Conclusion

So what is the point?  There is a collection of masks going downward like a Matryoshka doll.  I was satisfied I’d gotten close enough to the bottom of it when I burned my fingers.  The masks are there for a purpose.  The complexity of this endeavor is just too massive to take in all at once.  We must organize it by putting the masks on so that it can be learned one step at a time.
Consider now the fact that I’ve only talked about addition and only shown the wiring for a small part of even that.  It is all still inside a Black Box, as it were.  The relative number of people who can understand this is vanishingly small, and, as a wise friend of mine says, it is becoming increasingly like magic to the average person.
As a teacher, this motivates me.