M and E, Kepler’s Equation
In this section, we will at last have occasion to refer to Kepler’s Second Law which states that the segment from the sun to the planet sweeps out equal areas in equal times. This is to say that the area swept out is proportional to time, exactly as if the ellipse were a circle and exactly as if the planet were moving at a constant rate.
Before we explore this too deeply, let us discuss the matter of calculating the area of an ellipse and regions of an ellipse by making a relation to the circle.
Let us imagine our ellipse as having a semimajor axis of length $a$ and eccentricity $e$, and of sharing a center with a circle of radius $a$. We may impose a coordinate system wherein both have a center at the origin. In this case the circle and the ellipse have the following equations respectively:
and
It is a simple calculation to show that if $(x_0,y_0)$ is a point on the circle then
is a point on the ellipse. This multiplication of the $y$-coordinate corresponds to a vertical shrinking of the plane by a factor of
Suppose that $R_{CL}$ is some region of the circle and that $R_{EL}$ is the region of the ellipse obtained by this vertical shrinking. We may approximate the area of $R_{CL}$ by covering it with rectangles whose sides are parallel to the $x$- and $y$-axes, each of which has some area
Given an appropriately developed theory of area, which is beyond the scope of this work, it is easy to conclude that the area of $R_{EL}$ is
times the area of $R_{CL}$.
From this it follows that the area of an ellipse is
Having gotten a handle on the area of an ellipse, let us now relate it to Kepler’s Second Law. The value of Kepler’s Second Law resides in its relating area to time.
For a circle, the area of a sector can be used found by the formula
By allowing $\theta$ to vary from $0$ to $2\pi$, we can cover the whole circle. For our purposes, it will serve us well to think of $\theta$ as a linear function of $t$.
Then if we set
inserting the vertical shrinking factor of
we obtain a function which gives the area swept out by the segment from the sun to the planet in terms of time. Equal areas will be swept out in equal times, as promised by Kepler. It all depends on the value of $n$.
If we let $T$ denote the period of the planet, we know two things
and
Therefore,
Solving for $n$ gives us
So
I do not simplify this because I am interested in $\frac{2\pi}{T}t$ as a separate expression.
We will now define $M$, the mean anomaly, as
This $M$ is the key piece in determining $\nu$ in terms of time.
Let us now recall our circle-ellipse pair. We will ignore the coordinate system in favor of the synthetic approach.
We will determine an expression for $A_{\nu}$, the area of the region of the ellipse bounded the angle clockwise from the ray from $S$ to $H$ to the ray from $S$ to $P$. Let $A_E$ be the area of the circle bounded by the angle from the ray from $S$ to $H$ to the ray from $S$ to $P’$; this latter ray is not pictured in our diagram. However, let us note that
as the region in the circle can be shrunk to the second by multiplication by our shrink factor.
We may find the value of $A_E$ by reducing the area of the sector of the circle bound by the ray from $C$ to $H$ on one side and the ray from $C$ to $P’$ on the other by the area of the triangle $SCP’$. The area of the sector is
and the area of the triangle is
so
A comparison of this to the equations for $A(t)$ and $M$ will give us
Given a calculated value for $M$, the most practical way to solve for $E$ is to make use of Newton’s Method.
In the next section, we will relate $E$ to $\nu$.





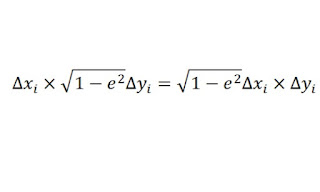













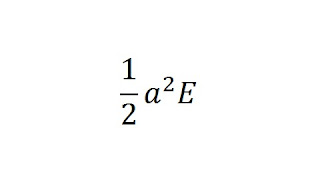








No comments:
Post a Comment